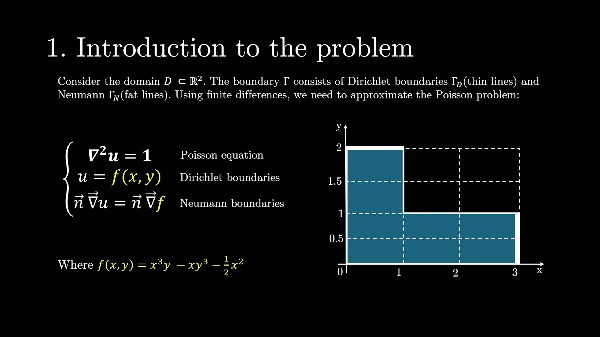
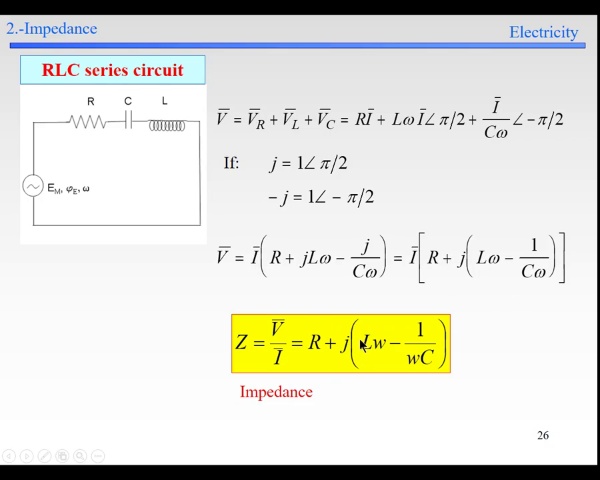
Differential Equations - Final Project

Using finite differences we solve Airy¿s equation ¿u/¿t=(¿^3 u)/(¿x^3 ). First, we investigate the four possible placements of the stencil (completely upwind, two points upwind¿one point down-wind, one point upwind¿two points downwind and completely downwind) for stability, using von Neumann stability analysis. Then, we implement the stable approximations in a Matlab program. Secondly, we derive a centred symmetric five-point stencil that approximates u_xxx, showing that it leads to an unstable method. The stability is recovered by adding a numerical diffusion term cu_xx and a numerical super-diffusion term -c*u_xxxx. Finally, using Lax-Friedrichs we approach and show that the new method is stable, given the constant c is chosen large enough.